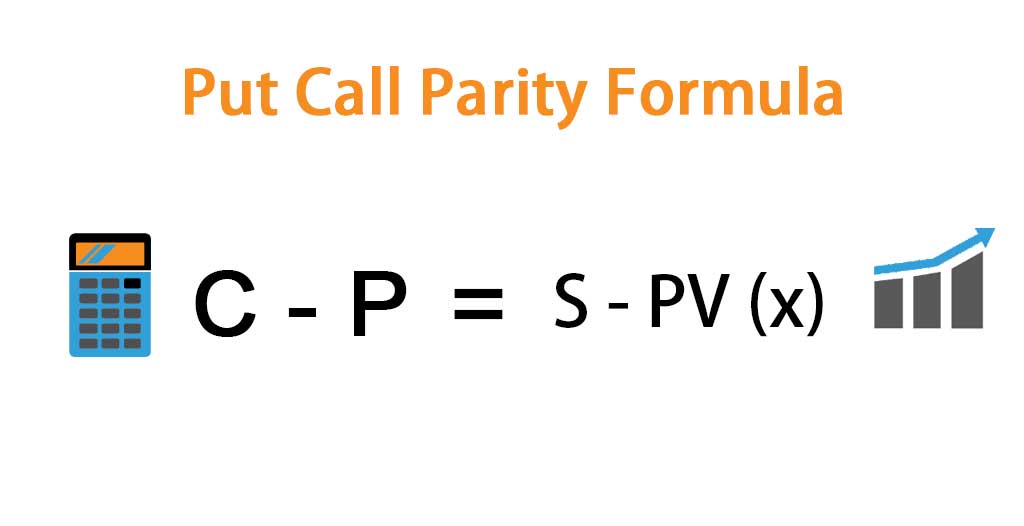Put-Call Parity

 

What is Put-Call Parity?

Put-Call parity theorem says that premium (price) of a call option implies a certain fair price for corresponding put options provided the put options have the same strike price, underlying and expiry and vice versa. It also shows the three-sided relationship between a call, a put, and underlying security. The theory was first identified by Hans Stoll in 1969.

Put-Call Parity Example

Let’s take a look at two portfolios of an investor:

Portfolio A: A European call options for a strike price of $500/- which has a premium or price of $80/- and pays no dividend (impact of dividend is discussed later in the paper) and A zero-coupon bond (which pays only principal at the time of maturity) which pays Rs.500/- (or the strike price of call options) at maturity and,

Portfolio B: Underlying stock on which call options are written and a European put options having an identical strike price of $500/- which has a premium of $80/- and an identical expiry.

In order to calculate pay-offs from both the portfolios, let’s consider two scenarios:

1. Stock price goes up and closes at $600/- at the time of maturity of an options contract,
2. The stock price has fallen and closes at $400/- at the time of maturity of an options contract. 

Impact on Portfolio A in Scenario 1: Portfolio A will be worth the zero-coupon bond I .e.$500/- plus $100/- from call options pay-off i.e. max(ST-X,0). Therefore, portfolio A will be worth the stock price (ST) at time T.

Impact on Portfolio A in Scenario 2: Portfolio A will be worth the share price i.e. $500/- since the stock price is less than the strike price (it is out of the money), the options will not be exercised. Hence, portfolio A will be worth stock price (ST) at time T.

Likewise, for portfolio B, we will analyze the impact of both scenarios.

Impact on Portfolio B in Scenario 1: Portfolio B will be worth the stock price or share price i.e. $600/- since the share price is lower than the strike price (X) and are worthless to exercise. Therefore, portfolio B will be worth the stock price (ST) at time T.

Impact on Portfolio B in Scenario 2: Portfolio B will be worth the difference between the strike price and stock price i.e. $100/- and underlying share price i.e. $400/-. Hence, portfolio B will be worth a strike price (X) at time T.

The above pay-offs are summarized below in Table 1.

Table: 1

		When ST > X	When ST < X
Portfolio A	Zero-Coupon bond	500	500
	Call option	100*	0
Total		600	500
Portfolio B	Underlying Stock (Share)	600	400
	Put option	0	100#
Total		600	500

*The pay-off of a call option = max(ST-X,0)

#The pay-off of a put option = max(X- ST,0)

In the above table we can summarize our findings that when the stock price is more than the strike price (X), the portfolios are worth the stock or share price (ST) and when the stock price is lower than the strike price, the portfolios are worth the strike price (X). In other words, both the portfolios are worth max(ST, X).

Portfolio A: When, ST > X, it is worth ST,

Portfolio B: When, ST < X, it is worth X

Since, both the portfolios have identical values at time T, they must, therefore, have similar or identical values today (since the options are European, it cannot be exercised prior to time T). And if this is not true an arbitrageur would exploit this arbitrage opportunity by buying the cheaper portfolio and selling the costlier one and book an arbitrage (risk-free) profit.

This brings us to a conclusion that today portfolio A should be equal to Portfolio B. or,

C0+X*e-r*t = P0+S0

Arbitrage Opportunity through Put-Call Parity

Let’s take an example to understand the arbitrage opportunity through put-call parity.

Suppose, the share price of a company is $80/-, the strike price is $100/-, the premium (price) of a six-month call option is $5/- and that of a put option is $3.5/-. The risk-free rate in the economy is 8% per annum.

Now, as per the above equation of put-call parity, the value of the combination of the call option price and the present value of strike would be,

C0+X*e-r*t = 5+100*e-0.08*0.5

= 101.08

And the value of the combination of put option and share price is

P0+S0 = 3.5+80

= 83.5

Here, we can see that the first portfolio is overpriced and can be sold (an arbitrageur can create a short position in this portfolio) and the second portfolio is relatively cheaper and can be bought (arbitrageur can create a long position) by the investor in order to exploit arbitrage opportunity.

This arbitrage opportunity involves buying a put option and a share of the company and selling a call option.

Let’s take this further, by shorting the call option and creating a long position in put option along with share would require below calculated funds to be borrowed by an arbitrageur at risk-free rate i.e.

= -5+3.5+80

= 78.5

Hence, an amount of $78.5 would be borrowed by the arbitrageur and after six months this needs to be repaid. Hence, the repayment amount would be

= 78.5*e0.08*0.5

= 81.70

Also, after six months either the put or call option would be in the money and will be exercised and arbitrageur would get $100/- from this. The short call and long call put option position would, therefore, lead to the stock being sold for $100/-. Hence, the net profit generated by the arbitrageur is

= 100 – 81.70

= $18.30

The above cash flows are summarized in Table 2:

Table: 2

Steps involved in arbitrage position	Cost involved
Borrow $78.5 for six months and create a position by selling one call option for $5/- and buying one put option for $3.5/- along with a share for $80/- i.e. (80+3.5-5)	-81.7
After six months, if the share price is more than the strike price, the call option would be exercised and if it is below the strike price then put option would be exercised	100
Net Profit (+) / Net Loss (-)	18.3

The Other side of Put-Call parity

Put-Call parity theorem only holds true for European style options as American style options can be exercised at any time prior to its expiry.

The equation which we have studied so far is

C0+X*e-r*t = P0+S0

This equation is also called as Fiduciary Call is equal to Protective Put.

Here, the left side of the equation is called Fiduciary Call because, in fiduciary call strategy, an investor limits its cost associated with exercising the call option (as to the fee for subsequently selling an underlying which has been physically delivered if the call is exercised).

The right side of the equation is called Protective Put because in a protective put strategy an investor is purchasing put option along with a share (P0+S0). In case, share prices go up the investor can still minimize their financial risk by selling shares of the company and protects their portfolio and in case the share prices go down he can close his position by exercising the put option.

For example:-

Suppose strike price is $70/-, Stock price is $50/-, Premium for Put Option is $5/- and that of Call Option is $15/-. And suppose that stock price goes up to $77/-.

In this case, the investor will not exercise its put option as the same is out of the money but will sell its share at the current market price (CMP) and earn the difference between CMP and the initial price of stock i.e. Rs.7/-. Had the investor not been purchased sock along with the put option, he would have been ended up incurring the loss of his premium towards option purchase.

Determining Call options & Put options premium

We can rewrite the above equation in two different ways as mentioned below.

• P0 = C0+X*e-r*t-S and
• C0 = P0+S0-X*e-r*t

In this way, we can determine the price of a call option and put option.

For example, let’s assume the price of an XYZ company is trading at Rs.750/- six months call option premium is Rs.15/- for the strike price of Rs.800/-. What would be the premium for put option assuming risk-free rate as 10%?

As per the equation mentioned above in point no 1,

P0 = C0+X*e-r*t-S

= 15+800*e-0.10*0.05-750

= 25.98

Likewise, suppose that in the above example put option premium is given as $50 instead of call option premium and we have to determine call option premium.

C0 = P0+S0-X*e-r*t

= 50+750-800*e-0.10*0.05

= 39.02

Impact of dividends on put-call parity

So far in our studies, we have assumed that there is no dividend paid on the stock. Therefore, the very next thing which we have to take into consideration is the impact of dividend on put-call parity.

Since interest is a cost to an investor who borrows funds to purchase stock and benefit to the investor who shorts the stock or securities by investing the funds.

Here we will examine how the Put-Call parity equation would be adjusted if the stock pays a dividend. Also, we assume that dividend which is paid during the life of the option is known.

Here, the equation would be adjusted with the present value of the dividend. And along with the call option premium, the total amount to be invested by the investor is cash equivalent to the present value of a zero-coupon bond (which is equivalent to the strike price) and the present value of the dividend. Here, we are making an adjustment in the fiduciary call strategy. The adjusted equation would be

C0+(D+X*e-r*t) = P0+ S0  where,

D = Present value of dividends during the life of

Let’s adjust the equation for both the scenarios.

For example, suppose the stock pays $50/- as dividend then, adjusted put option premium would be

P0 = C0+(D+X*e-r*t) – S0

   = 15+(50*e-0.10*0.5+800*e-0.10*0.5)-750

= 73.54

We can adjust the dividends in another way also which will yield the same value. The only basic difference between these two ways is while in the first one we have added the amount of the dividend in strike price, in the other one we have adjusted the dividends amount directly from the stock.

P0 = C0+X*e-r*t– S0-(S0*e-r*t),

In the above formula, we have deducted the amount of the dividend (PV of dividends) directly from the stock price. Let’s look at the calculation through this formula

= 15+800*e-0.10*0.5-750-(50*e-0.10*0.5)

= 73.54

Concluding Remarks

• Put-Call parity establishes the relationship between the prices of European put options and calls options having the same strike prices, expiry and underlying.
• Put-Call Parity does not hold true for the American option as an American option can be exercised at any time prior to its expiry.
• Equation for put-call parity is C0+X*e-r*t = P0+S0.
• In put-call parity, the Fiduciary Call is equal to Protective Put.
• Put-Call parity equation can be used to determine the price of European call and put options
• Put-Call parity equation is adjusted if the stock pays any dividends.